Metodo di fattorizzazione di Eulero

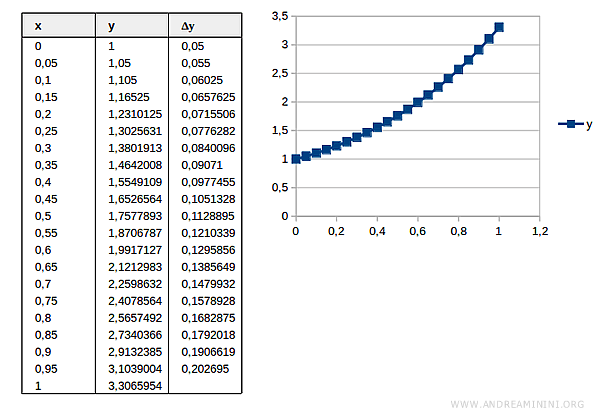
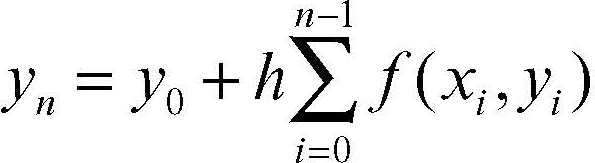Il metodo di fattorizzazione di Eulero è un algoritmo ideato da Eulero per fattorizzare dei numeri naturali in numeri primi.

Si basa sulla rappresentazione del numero n (da fattorizzare) come somma di due quadrati in due modi distinti, e per questo non è applicabile né a numeri nella forma 4k 3, né a quelli in cui un numero primo di questa forma è presente ad un esponente dispari nella fattorizzazione di n. Questo ne riduce grandemente il campo di applicabilità, perché anche molti semiprimi nella forma 4k 1 sono prodotto di due primi del tipo 4k 3.

Per questo motivo non è spesso usato come metodo di fattorizzazione, perché non è possibile sapere a priori se un dato numero sia o meno fattorizzabile con quest'algoritmo.

Algoritmo

Data una doppia scrittura di n come somma di due quadrati:

${\displaystyle n=a^{2} b^{2}=c^{2} d^{2}}$

(a, b, c e d possono essere trovati, ad esempio, con delle tavole dei quadrati) e supponendo che b e d abbiano la stessa parità (cioè siano entrambi pari o entrambi dispari), e che a sia maggiore di c (e conseguentemente d maggiore di b) si ha

${\displaystyle a^{2}-c^{2}=(a-c)(a c)=(d-b)(d b)=d^{2}-b^{2}}$

(a-c) e (d-b) sono entrambi pari, e quindi hanno un massimo comun divisore k non banale (che può essere trovato velocemente con l'uso dell'algoritmo euclideo); ponendo

${\displaystyle a-c=kA,~~~d-b=kB}$

risulta che A e B sono coprimi. Sostituendo si ha

${\displaystyle kA(a c)=kB(d b)}$

e quindi, per il lemma di Euclide, A divide d b e B divide a c, e in particolare, se ${\displaystyle a c=BC}$,

${\displaystyle kABC=kB(d b)\Longrightarrow AC=d b}$.

A questo punto, considerando la quantità

${\displaystyle \left[\left({\frac {k}{2}}\right)^{2} \left({\frac {C}{2}}\right)^{2}\right]\cdot (A^{2} B^{2})}$

e svolgendo i conti, questa risulta essere uguale a n, e quindi è una sua fattorizzazione non banale.

Collegamenti esterni

• (EN) Eric W. Weisstein, Euler's Factorization Method, su MathWorld, Wolfram Research.