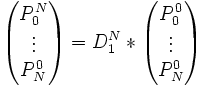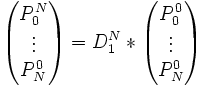Algoritmo di de Casteljau

In matematica e in particolare in analisi numerica, l'algoritmo di de Casteljau, che prende il nome dal suo autore Paul de Casteljau, è un metodo ricorsivo per valutare polinomi nella forma di Bernstein o curve di Bézier.

Sebbene l'algoritmo sia più lento per la maggior parte delle architetture se comparato all'approccio diretto, è numericamente più stabile.

Definizione

Dato un polinomio B in forma di Bernstein di grado n

${\displaystyle B(t)=\sum _{i=0}^{n}\beta _{i}b_{i,n}(t),}$

dove b è un polinomio base di Bernstein, il polinomio al punto t₀ può essere valutato con la relazione di ricorrenza

${\displaystyle \beta _{i}^{(0)}:=\beta _{i}{\mbox{ , }}i=0,\ldots ,n,}$

${\displaystyle \beta _{i}^{(j)}:=\beta _{i}^{(j-1)}(1-t_{0}) \beta _{i 1}^{(j-1)}t_{0}{\mbox{ , }}i=0,\ldots ,n-j{\mbox{ , }}j=1,\ldots n,}$

con

${\displaystyle B(t_{0})=\beta _{0}^{(n)}.}$

Annotazioni

Nel calcolo manuale è utile scrivere i coefficienti in uno schema triangolare del tipo:

${\displaystyle {\begin{matrix}\beta _{0}&=\beta _{0}^{(0)}&&&\\&&\beta _{0}^{(1)}&&\\\beta _{1}&=\beta _{1}^{(0)}&&&\\&&&\ddots &\\\vdots &&\vdots &&\beta _{0}^{(n)}\\&&&&\\\beta _{n-1}&=\beta _{n-1}^{(0)}&&&\\&&\beta _{n-1}^{(1)}&&\\\beta _{n}&=\beta _{n}^{(0)}&&&\\\end{matrix}}}$

Nella scelta di un punto t₀ per cui calcolare il polinomio di Bernstein, si possono usare le diagonali dello schema triangolare per costruire una divisione del polinomio.

${\displaystyle B(t)=\sum _{i=0}^{n}\beta _{i}^{(0)}b_{i,n}(t)\qquad {\mbox{ , }}\in [0,1],}$

fino a

${\displaystyle B_{1}(t)=\sum _{i=0}^{n}\beta _{0}^{(i)}b_{i,n}\left({\frac {t}{t_{0}}}\right)\qquad {\mbox{ , }}\in [0,t_{0}]}$

e

${\displaystyle B_{2}(t)=\sum _{i=0}^{n}\beta _{n-i}^{(i)}b_{i,n}\left({\frac {t-t_{0}}{1-t_{0}}}\right)\qquad {\mbox{ , }}\in [t_{0},1].}$

Esempio

Si vuole calcolare il valore del polinomio di Bernstein di grado 2 con i coefficienti:

${\displaystyle \beta _{0}^{(0)}=\beta _{0}}$

${\displaystyle \beta _{1}^{(0)}=\beta _{1}}$

${\displaystyle \beta _{2}^{(0)}=\beta _{2}}$

nel punto t₀.

Si avvia la ricorsione con:

${\displaystyle \beta _{0}^{(1)}=\beta _{0}^{(0)}(1-t_{0}) \beta _{1}^{(0)}t_{0}=\beta _{0}(1-t_{0}) \beta _{1}t_{0}}$

${\displaystyle \beta _{1}^{(1)}=\beta _{1}^{(0)}(1-t_{0}) \beta _{2}^{(0)}t_{0}=\beta _{1}(1-t_{0}) \beta _{2}t_{0}}$

e alla seconda iterazione la ricorsione termina con:

${\displaystyle {\begin{matrix}\beta _{0}^{(2)}&=&\beta _{0}^{(1)}(1-t_{0}) \beta _{1}^{(1)}t_{0}\\\ &=&\beta _{0}(1-t_{0})(1-t_{0}) \beta _{1}t_{0}(1-t_{0}) \beta _{1}(1-t_{0})t_{0} \beta _{2}t_{0}t_{0}\\\ &=&\beta _{0}(1-t_{0})^{2} \beta _{1}2t_{0}(1-t_{0}) \beta _{2}t_{0}^{2}\\\end{matrix}}}$

che è il polinomio di Bernstein desiderato di grado 2.

Altri progetti

• Wikimedia Commons contiene immagini o altri file su Algoritmo di de Casteljau